Μια από τις πιο εντυπωσιακές μορφές στον χώρο των μαθηματικών αποτελεί ο Ινδός «αυτοδίδακτος» μαθηματικός Srinivasa Ramanujan (Ραμανουτζάν) (1887 – 1920). Παρά τη σύντομη διάρκεια της «μαθηματικής» ζωής του, άφησε πίσω του ένα έργο που απασχολεί ακόμη μαθηματικούς και φυσικούς – παρότι το μεγαλύτερο μέρος του ανακαλύφθηκε με έναν εντελώς διαισθητικό και μυστηριώδη τρόπο.
Ο βραβευμένος με Νόμπελ φυσικός Steven Weinberg θυμάται
ότι στις αρχές της δεκαετίας του 1970, όταν μελετούσε τη – δημοφιλή
σήμερα – θεωρία των χορδών, αντιμετώπισε το πρόβλημα του υπολογισμού του
πλήθους p(n) των αναλύσεων σε άθροισμα του n, όταν το n είναι μεγάλο.
Αποδείχθηκε ότι όλοι οι τύποι που χρειαζόταν είχαν ανακαλυφθεί από τον
Ramanujan το 1918!
Το p(n) δίνει το πλήθους των τρόπων με τους οποίους μπορούμε να παραστήσουμε τον αριθμό n ως άθροισμα φυσικών αριθμών.
Για παράδειγμα, p(4) = 5
4 = 3 +1 = 2 +2 = 2 + 1 + 1 = 1 + 1 + 1 + 1
Η διαδικασία με
μια πρώτη ματιά φαίνεται πανεύκολη, όμως όταν αριθμός n που πρέπει να
διαμερίσουμε αυξάνεται, αυξάνεται και το πλήθος των διαμερίσεών p(n).
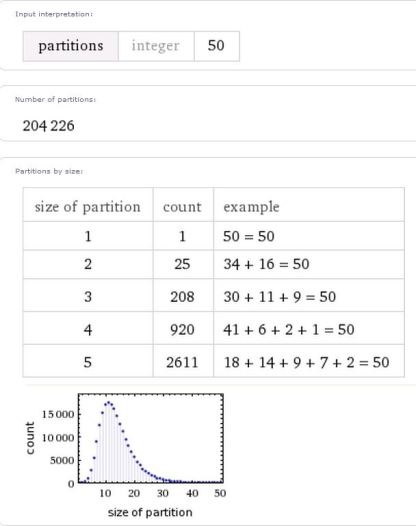
Αν n = 10 τότε p(10) = 42
Αν n = 30 τότε p(30) = 5604
Αν n = 40 τότε p(40) = 37338
Αν n = 50 τότε p(50) = 204226
και αν
Αν n = 100 τότε p(100) = 190569292
To p(n) (για πολύ μεγάλα n) προσεγγίζεται από τον τύπο
Μια βελτιωμένη προσέγγιση του p(n) προέκυψε από την διόρθωση που «οραματίστηκε» ο Ramanujan:
όπου ο παράγοντας
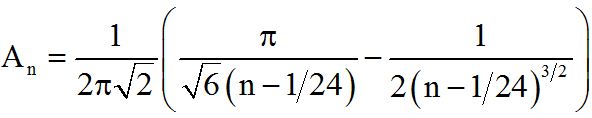
είναι επίσης συνάρτηση του n.
To εντυπωσιακό με τον παραπάνω τύπο είναι ότι ενώ είναι «προσεγγιστικός»,
για n= 200 δίνει p(n)=3972999029388
που ταυτίζεται με την πραγματική τιμή!
Το ακόμα πιο μυστηριώδες στην εξίσωση είναι η μικρή διόρθωση (-1/24) που είχε προτείνει ο Ramanujan. Κανείς, ούτε καν ο Ramanujan, μπορούσε να εξηγήσει γιατί εμφανίζεται. Πάντως, αυτή η μυστήρια διόρθωση έκανε τον τύπο να δουλεύει. Ο Hardy και ο Ramanujan δεν σταμάτησαν στον προσεγγιστικό τύπο. Αργότερα ανακάλυψαν μια ακριβή ισότητα για το p(n).
Σύμφωνα με το newscientist ένας
νέος τύπος βγαλμένος από τις «μυστηριώδεις» εμπνεύσεις του Srinivasa
Ramanujan, θα μπορούσε να βελτιώσει την κατανόησή μας σχετικά με τις
μαύρες τρύπες.
Επ’ ευκαιρίας της 125ης επετείου
από τη γέννηση του , ο Ken Ono του Πανεπιστημίου Emory στην Ατλάντα, ο
οποίος παλιότερα είχε ανακαλύψει τα μυστηριώδη βήματα στη σκέψη του
Ramanujan, εξέτασε για άλλη μια φορά τις σημειώσεις και τις επιστολές
του (ένα πιο τεχνικό άρθρο μπορείτε να διαβάσετε ΕΔΩ: mathcs.emory.edu).
Ο Ken Ono επικέντρωσε το ενδιαφέρον του, στην τελευταία γνωστή επιστολή που έγραψε ο Ramanujan προς τον Hardy, σχετικά με ένα είδος συναρτήσεων που αποκαλούνται modular μορφές. Aυτές οι συναρτήσεις χρησιμοποιούνται σήμερα στον υπολογισμό της εντροπίας των μαύρων τρυπών. Η ιδιότητα αυτή συνδέεται με την εκπληκτική πρόβλεψη του Stephen Hawking ότι οι μαύρες τρύπες εκπέμπουν ακτινοβολία.
Για τον αναγνώστη που δεν γνωρίζει το
φαινόμενο Ramanujan, παραθέτουμε στη συνέχεια ένα απόσπασμα από τον
πρόλογο που έγραψε ο Γιώργος Λ. Ευαγγελόπουλος για την ελληνική έκδοση
του βιβλίου «ΡΑΜΑΝΟΥΤΖΑΝ, Ο Ινδός Μαθηματικός, Robert Kanigel, εκδόσεις Τραυλός»
(….)Η περίπτωση του Βραχμάνου Ινδού, Srinivasa Ramanujan (1887 – 1920), αποτελεί μια από τις πιο σπάνιες περιπτώσεις εξαίρετης δημιουργικότητας στην ιστορία της μαθηματικής επιστήμης. Ίσως την πιο αξιοσημείωτη, από την άποψη της πρωτοτυπίας του έργου που παρήγαγε ως αυτοδίδακτος – μέχρι τα είκοσι έξι του χρόνια μαθηματικός!
Μετά την επιτυχή ολοκλήρωση των
γυμνασιακών του σπουδών, αφοσιώθηκε πλήρως στη μελέτη των μαθημάτων που
απαιτούνταν για την απόκτηση πτυχίου πανεπιστημιακού κολεγίου.
Εμπνεόμενος από τη μελέτη ενός εγχειριδίου, δούλεψε μόνος του και
παρήγαγε μια σειρά από θεωρήματα και άλλα μαθηματικά αποτελέσματα,
κυρίως στη θεωρία αριθμών. Η αποτυχία του, όμως, να αποκτήσει
πανεπιστημιακό τίτλο σπουδών, που δυσχέραινε πολύ την προσπάθεια
ανεύρεσης εργασίας, αλλά κυρίως η επιφυλακτικότητα έως απόρριψη που
γνώρισε στην προσπάθειά του να πετύχει αναγνώριση της αξίας του έργου
του από συμπατριώτες του μαθηματικούς (με την ευχάριστη έκπληξη
ελάχιστων εξαιρέσεων), παρ’ ολίγο να οδηγήσουν σε άδοξο τέλος τη
σταδιοδρομία του.
Όλα άλλαξαν, όταν ο G. H. Hardy (1877 –
1947), ένας από τους δυο πιο σημαντικούς Άγγλους μαθηματικούς της εποχής
του – ο άλλος ήταν ο φίλος και συνεργάτης του σε σειρά κοινών
μαθηματικών δημοσιεύσεων, J. E. Littlewood, εταίρος κι αυτός, όπως και ο
hardy, τόσο του Κολεγίου Τρίνιτι του Πανεπιστημίου του Κέμπριτζ, όσο
και της Βασιλικής Εταιρείας του Λονδίνου – έλαβε μια επιστολή από τον
Ramanujan που συνοδευόταν από πολλές σελίδες με μαθηματικά θεωρήματα.
Ο Hardy σε αντίθεση με δυο εκλεκτούς
συναδέλφους του που έλαβαν ανάλογου περιεχομένου επιστολές από τον
Ramanujan και προφανώς αδιαφόρησαν, καταπιάστηκε (από κοινού με τον
Littlewood, του οποίου ζήτησε και έλαβε τη βοήθεια) με τη μελέτη και την
κατανόηση των μαθηματικών αποτελεσμάτων που περιείχε η επιστολή. Αρκετά
από αυτά τα αποτελέσματα ήταν νέα, ενώ συχνά έμοιαζαν και απολύτως
δυσνόητα, τουλάχιστον ως προς τον «αποδεικτικό» συλλογισμό που τα
στήριζε. Η απόδειξη, με την αυστηρή έννοια του όρου (αυτή που αποτέλεσε
τη μεγαλύτερη συμβολή της αρχαίας ελληνικής μαθηματικής επιστήμης στον
τρόπο με τον οποίο κάνουμε μαθηματικά σήμερα), ήταν άγνωστη στον
Ramanujan. Οι «αποδείξεις» του ήταν απολύτως ιδιόμορφης φύσεως και
στηρίζονταν κυρίως στη διαίσθησή του, που τον οδηγούσε πάντοτε σε μια
σειρά «περίεργων» βημάτων στο πλαίσιο μιας εντελώς δικής του
συλλογιστικής. Αλλά και όσα μαθηματικά αποτελέσματα ήταν γνωστά,
προκάλεσαν κι αυτά την έκπληξη και το θαυμασμό του Hardy, διότι
αποτελούσαν εκ νέου ανακαλύψεις γνωστών αποτελεσμάτων που παρήγαγαν
μεγάλοι μαθηματικοί του παρελθόντος (για παράδειγμα ο Euler).
Oι Hardy και Littlewood αντιλήφθηκαν
αμέσως ότι ο νεαρός Ινδός επιστολογράφος συνιστούσε άκρως ενδιαφέρουσα
περίπτωση πρωτότυπης ιδιοφυίας. Μάλιστα, έπειτα από την ανταλλαγή
κάποιων ακόμη επιστολών μαζί του, ο Hardy οργάνωσε και μεθόδευσε – μέσω
της αποστολής του συναδέλφου μαθηματικού, E. H. Neville, στην Ινδία γι’
αυτόν ακριβώς το σκοπό – την πρόσκληση του Ramanujan στο Κολέγιο Τρίνιτι
του Κέμπριτζ. Ύστερα από μια πρώτη, πρόσκαιρη άρνηση, ο Ramanujan
δέχτηκε να πάει στο Κέμπριτζ, όπου έφτασε τον Απρίλιο του 1914. Εκεί,
σύμφωνα με το πρόγραμμα που του είχε ετοιμάσει ο Hardy, o Ramanujan
παρακολούθησε κάποιες διαλέξεις στην Ανάλυση (προϋπόθεση απαραίτητη για
να μπορέσει να κατανοήσει την αναλυτική θεωρία αριθμών) και,
δευτερευόντως, στην άλγεβρα, ώστε να μπορέσει κατόπιν να συνεργαστεί –
επί ίσοις όροις – με τους Littlewood και Hardy. Επιπλέον, αρκετά
μαθηματικά του τα δίδαξε κατ’ ιδίαν ο Hardy στη διάρκεια των συναντήσεών
τους. Γενναιόδωρος, όμως, και ειλικρινής, καθώς ήταν, παραδέχθηκε ότι
«προφανώς εγώ διδάχθηκα περισσότερα από εκείνον απ΄όσα αυτός [ο
Ramanujan] από εμένα».
Τα χρόνια του Κέμπριτζ υπήρξαν παραγωγικά
για τον Ramanujan, αλλά δεν διήρκεσαν πολύ. Την άνοιξη του 1917
αρρώστησε και νωρίς το καλοκαίρι μπήκε στο νοσοκομείο. Ακολουθώντας
ιατρική σύσταση, επέστρεψε στην Ινδία στις αρχές του 1919, και πέθανε
εκεί τον Απρίλιο του 1920. Πέρασε τα τρία τελευταία χρόνια της ζωής του
σε σανατόρια, με την υγεία του σε κακή κατάσταση. Παρ’ όλα αυτά, ήταν
μόλις το 1918 που ανακάλυψε μερικά από τα πιο ωραία του θεωρήματα, την
εποχή περίπου που εκλέχτηκε εταίρος της Βασιλικής Εταιρείας του
Λονδίνου.
Το διάστημα που ο Ramanujan διέθετε τη
χρονική άνεση και ήταν υγιής, ώστε να μπορεί να ασχολείται ανεμπόδιστα
με τα μαθηματικά, δεν υπερέβη τελικώς τα τέσσερα χρόνια, ενώ η συνολική
διάρκεια της ζωής του ως «επαγγελματία μαθηματικού» ήταν επτά περίπου
έτη (αρχίζοντας από τη μετάβασή του στο Κέμπριτζ).
Στα προσκόμματα που αντιμετώπισε σ’ αυτά
τα χρόνια πρέπει να συνυπολογιστούν και οι δυσκολίες που επέφερε στη
διεξαγωγή της έρευνάς του, ο Πρώτος Παγκόσμιος Πόλεμος, με κυριότερη την
αναγκαστική προσωρινή διακοπή της συνεργασίας του με τον Littlewood, ο
οποίος άφησε το Κέμπριτζ, για να προσφέρει τις καλές του υπηρεσίες στον
αγγλικό στρατό.
Το ερώτημα για το πόσο μεγάλος μαθηματικός
υπήρξε πράγματι ο Ramanujan ή πόσο μεγάλος θα μπορούσε να είχε γίνει,
εάν είχε την τύχη να λάβει οργανωμένη μαθηματική εκπαίδευση, έχει τεθεί
επανειλημμένα από μαθηματικούς και ιστορικούς της επιστήμης, από το
θάνατό του μέχρι σήμερα, εν όψει μάλιστα των συνεχών επαναξιολογήσεων
του μαθηματικού έργου.
Ο C. P. Snow στον πρόλογό του κλασικό
βιβλίο του G. H. Hardy, «Η απολογία ενός Μαθηματικού», σημειώνει ότι οι
Hardy και Littlewood, μελετώντας τις επιστολές του Ramanujan, κατέληξαν
στο συμπέρασμα ότι «ο συγγραφέας των χειρογράφων είναι ιδιοφυής». Και
συνεχίζει: «Ήταν μόνο αργότερα που ο Hardy αποφάσισε ότι ο Ramanujan
ανήκε, όσον αφορά στην έμφυτη μαθηματική του ιδιοφυία, στην κλάση του
Gauss και του Euler, με τη μόνη διαφορά ότι δεν μπορούσε να αναμένει,
λόγω των κενών στην εκπαίδευσή του και επειδή εμφανίστηκε πολύ αργά στο
προσκήνιο της ιστορίας των μαθηματικών, να συμβάλλει σε ίση κλίμακα».
Την άποψη αυτή αμφισβήτησε ο Ι. J.
Mordell, υποστηρίζοντας ότι είναι κάπως δύσκολο να δεχθούμε ότι ο Hardy
έκανε την παραπάνω δήλωση που ο Snow του αποδίδει. Και αυτό διότι ο
Ramanujan διακρίθηκε σε ορισμένους τομείς των μαθηματικών και είχε
αναντίρρητα, απίστευτο μαθηματικό ταλέντο, πλην όμως η σύγκρισή του με
τους Gauss και Euler είναι υπερβολική, αν αναλογιστούμε την πολύπλευρη
και καθοριστική συνεισφορά των τελευταίων σε πολλούς κλάδους της
μαθηματικής επιστήμης. Τούτο είναι αληθές εάν σκεφτούμε ότι οι συμβολές
του Ramanujan στα μαθηματικά αφορούν στη μαθηματική Ανάλυση, τη θεωρία
αριθμών, τις απειροσειρές και τα συνεχή κλάσματα.
Θεωρώ, όμως, λιγότερο αφοριστική από τις
προηγούμενες και, ταυτοχρόνως, περισσότερο εκλεπτυσμένη στις διακρίσεις
που επιχειρεί – άρα και πιο ακριβοδίκαιη – τη σχετική κρίση του Hardy
που περιέχεται στο ακόλουθο απόσπασμα από ομιλία του στο Πανεπιστήμιο
του Χάρβαρντ, στις 31 Αυγούστου 1936: «Οι γνώμες μπορεί να διαφέρουν
όσον αφορά στη σπουδαιότητα του έργου του Ramanujan, το είδος του
κριτηρίου με το οποίο θα αξιολογηθεί, καθώς και την επιρροή που
ενδέχεται να ασκήσει στα μαθηματικά στο μέλλον. Δεν έχει την απλότητα
και τη «μονιμότητα»(inevitableness) του κατ’ εξοχήν μέγιστου έργου. Θα
μπορούσε να είναι μεγαλύτερο, εάν ήταν λιγότερο παράξενο. Το χάρισμα που
διαθέτει και το οποίο κανείς δεν μπορεί να αρνηθεί, είναι η βαθιά και
«ακατανίκητη» πρωτοτυπία. θα μπορούσε πιθανόν να είχε γίνει μεγαλύτερος
μαθηματικός, εάν ήταν δυνατόν να «συλληφθεί» και να «δαμαστεί» λίγο κατά
τη νεότητά του. Θα είχε ανακαλύψει περισσότερα τα οποία θα ήταν
καινούρια, και αναμφίβολα, μεγαλύτερης σπουδαιότητας. Από την άλλη, θα
ήταν λιγότερο “ο Ramanujan”, ενώ θα έμοιαζε περισσότερο σε Ευρωπαίο
Καθηγητή, και αυτό που θα χάναμε θα μπορούσε να ήταν μεγαλύτερο από αυτό
που θα κερδίζαμε…».
Επειδή έχει ήδη γίνει λόγος για τις
συνεχείς επαναξιολογήσεις του έργου του Ramanujan, κλείνοντας τη
συζήτηση για την αποτίμηση της συμβολής του στη μαθηματική επιστήμη,
αξίζει να παραθέσουμε τον ακόλουθο «Επίλογο» από άρθρο του Bruce C.
Bernt, διότι απαντά στις επιφυλάξεις του Hardy όσον αφορά στη
«μονιμότητα» της θέσης των μαθηματικών του Ramanujan στη σύγχρονη
μαθηματική επιστήμη: «Σε συζητήσεις για τον Ramanujan, εγείρεται
αναπόφευκτα το ερώτημα “Πόσο πραγματικά μεγάλος μαθηματικός υπήρξε;”
Στις περιοχές των απειροσειρών, των ελλειπτικών συναρτήσεων και των
συνεχών κλασμάτων, πολύ λίγοι στην ιστορία των μαθηματικών υπήρξαν
ισάξιοί του. Η κρίση μας, ωστόσο, κάπως “θαμπώνει”, λόγω της παράξενης
φύσης των “αποδείξεών” του.
Ο Hardy θεώρησε ότι “”Αυτό (τα μαθηματικά
του Ramanujan) δεν έχει την απλότητα και τη ‘μονιμότητα’
(inevitableness) του κατ’ εξοχήν μέγιστου έργου. Θα μπορούσε να είναι
μεγαλύτερο, εάν ήταν λιγότερο παράξενο”. Μεγάλο μέρος του έργου του
Ramanujan το οποίο δεν φαινόταν “μόνιμο” (inevitable) τον καιρό που
ανακαλύφθηκε έχει τώρα καταστεί περισσότερο “μόνιμο”, καθώς βλέπουμε
πόσο “δένει” με τα υπόλοιπα μαθηματικά. Έτσι, η ώρα της τελικής κρίσης
δεν είναι ακόμη κοντά. Αλλά, όσον αφορά στην αγάπη και την αφοσίωση του
Ramanujan στα μαθηματικά, δεν υπάρχει καμιά αμφιβολία…».
Εν κατακλείδι, λοιπόν, είναι η ίδια η
εξέλιξη της μαθηματικής επιστήμης που θα αναδείξει το μέγεθος της
συνεισφοράς του Ramanujan σ’ αυτήν (…)
ΠΗΓΕΣ
1. www.wolframalpha.com
2. ΡΑΜΑΝΟΥΤΖΑΝ, Ο Ινδός Μαθηματικός, Robert Kanigel, εκδόσεις Τραυλός
3. Περιοδικό QUANTUM, Μάιος/Ιούνιος 1998, ΤΟΜΟΣ 5/ ΤΕΥΧΟΣ 3
4. Mathematical proof reveals magic of Ramanujan’s genius, newscientist.com – Jacob Aron
5. ADDITION AND COUNTING: THE ARITHMETIC OF PARTITIONS,
Scott Ahlgren and Ken Ono

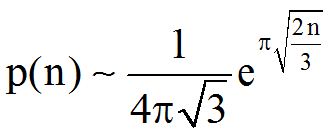
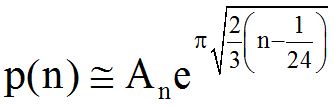
Δεν υπάρχουν σχόλια:
Δημοσίευση σχολίου